Varios de ustedes sabrán que la matemática es algo más que un hobby para mí. Son esas cosas inexplicables del cerebro humano que te llevan a pensar que sos mejor para una cosa que para la otra. Lo cierto es que según dicen, yo no hago cálculos como la mayoría de la gente. No sé si es bueno o es malo, pero muchas veces me encuentro resolviendo modelos matemáticos como un pasatiempo, mientras mis eventuales vecinos me miran espantados.

Tuve la enorme suerte de estudiar en la Facultad de Ciencias Exactas y Naturales de la Universidad de Buenos Aires, la Licenciatura en Ciencias Matemáticas. La calidad de los profesores de esa casa de estudio es única; pero en Exactas, había verdaderos titanes. Dentro de esos colosos, está nada más ni nada menos que Don Adrian Paenza. Si nunca leyeron uno de sus libros, o miraron alguno de sus programas en televisión, de verdad se están perdiendo a alguien muy interesante. Él explica la matemática que está encerrada en nuestras cosas cotidianas. Sí, en todo, hay matemática. Te puede explicar cómo armar el fixture de un torneo de fútbol, la frecuencia con la que deben circular los colectivos, o si hay vino en el agua o agua en el vino. Quiero tomarme el atrevimiento de «tomarle prestado» este ejercicio y al tiempo que se distraen un rato, invitarlos a que lean sus libros que están disponibles para ser descargados en formato pdf, de forma gratuita, en la página de Exactas. Con ustedes, el artículo:

¿Hay más agua en el vino o vino en el agua?
Este problema enseña a pensar (por supuesto, en un caso particular). La idea es educar la intuición y poder decidir mejor en aquellas situaciones de la vida en las que uno tiene que optar.
Caminaba por la Facultad de Exactas de la UBA y me encontré con Teresita Krick, matemática, profesora también y, sobre todo, muy buena amiga.
–Adrián, tengo un problema interesante para vos. ¿Tenés tiempo para que te lo cuente? Te va a servir para el final de cada programa de televisión –me dijo en un descanso de la escalera.
–Sí –le contesté–. Bienvenida sea toda historia que sirva para pensar.

–Bueno, la historia es así: se tienen dos vasos iguales. Uno contiene vino (llamémoslo V) y el otro agua (llamado A). Los dos tienen la misma cantidad de líquido. Uno toma una cuchara y la hunde en el vino. La llena (a la cuchara) y, sin que se caiga nada, vierte el vino que sacó en el vaso que contiene el agua y
revuelve. Es decir, mezcla el agua y el vino. Claramente, el vaso A tiene ahora un poco más de líquido que el vaso V. Más aún, lo que le falta de líquido a V, lo tiene de más el vaso A. ”Ahora bien –siguió Teresa–. Una vez que uno revolvió bien el contenido del vaso A, vuelve a meter la cuchara en el vaso A
y una vez más llena la cuchara. Claramente, lo que uno está eligiendo ahora, no es agua pura sino una mezcla. Pero no importa. Llena la cuchara con ese líquido y lo pone en el vaso V. Teresita me miraba fijo. Yo todavía no sabía hacia dónde iba, pero la dejé seguir:
–Si mezclamos otra vez el líquido en el vaso V, ¿qué te parece que pasa ahora? ¿Hay más agua en el vino o más vino en el agua?
Fin del problema. Ahora, a pensar.

El enunciado no contiene trucos ni trampas. Se supone que el agua y el vino no se mezclan, en el sentido de que no cambian sus propiedades. Sé que esto no es cierto, pero a los efectos del problema vamos a suponerlo así.

SOLUCIONES:
La cantidad de agua en el vino es la misma que la cantidad de vino en el agua.
¿Cómo convencerse de que esto es cierto? Hay varias maneras de pensar este problema. Yo voy a sugerir tres.

Primera solución:
Las cantidades de líquido que había en cada vaso eran originariamente las mismas. Además, y esto es importante, las cantidades de líquido que hay al final, luego de haber mezclado en ambos vasos, también es igual. Ahora bien: está claro que algo de vino quedó en el vaso A. Pero también es claro que algo de agua quedó en el vaso V. Ese algo de agua que falta en el vaso A está en V. Y ese algo de vino que falta en el vaso V está en A. Si esas cantidades no fueran iguales, querría decir que en uno de los dos vasos hay más líquido. Y eso no puede ser. Como las cantidades finales son las mismas, entonces, eso implica que lo
que falta de agua en el vaso A es igual a lo que falta de vino en el vaso V. Y eso era lo que queríamos demostrar.

Segunda solución:
En esta solución voy a ponerles nombres a los datos. A los vasos los hemos llamado A y V.

Llamemos:
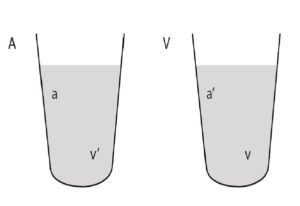
a = cantidad de agua que quedó en el vaso A luego del proceso.
a’ = cantidad de agua que quedó en el vaso V luego del proceso.
v = cantidad de vino que quedó en el vaso V luego del experimento.
v’ = cantidad de vino que quedó en el vaso A luego del experimento.

Entonces, se tienen estas igualdades:
(1) a + v’ = v + a’
Esto sucede porque las cantidades finales de líquido en cada vaso luego del experimento son las mismas.
Por otro lado:
(2) a + a’ = v + v’
Esto es cierto porque las cantidades iniciales de líquido en cada vaso eran iguales.
Pero, además, y éste es el dato clave, uno sabe que
(3) a + v’ = a + a’
ya que en el vaso A la cantidad de agua que había originariamente (a + a’) tiene que ser igual a la cantidad de líquido que hay luego del experimento, que es (a + v’). Con estos datos, estamos en condiciones de resolver el problema.

De la ecuación (3) se puede simplificar a, y entonces queda que
v’ = a’
que es lo que queríamos demostrar.

Tercera solución:
Vamos a hacer un modelo distinto sobre el mismo problema.
En lugar de líquido, vamos a suponer que hay bolitas de distintos colores en cada vaso.
Supongamos que en el vaso V hay 1.000 bolitas verdes y en el vaso A, 1.000 bolitas azules. Tomamos una cuchara y sacamos del vaso V, 30 bolitas (verdes) y las pasamos al vaso A (en donde están las azules). Ahora, en el vaso V quedan 970 bolitas (todas verdes) y en el vaso A, 1.030 bolitas (1.000 azules y 30 verdes que acabo de pasar con la cuchara). Mezclamos las bolitas del vaso A. En su mayoría son azules, pero ahora hay también 30 bolitas verdes.
Para replicar lo que hacíamos con el agua y el vino, volvemos a usar la cuchara. La hundimos en el vaso A, donde están las 1.030 bolitas, y a los efectos de avanzar con el pensamiento, vamos a suponer que nos llevamos 27 azules y 3 de las verdes que habían pasado antes (estos números son arbitrarios).
Volvemos a depositar estas 30 bolitas en el vaso V. Por favor, tome nota de que en el vaso A quedaron ahora 973 azules y 27 verdes. Ahora, al haber pasado las 30 bolitas del vaso A al V, los dos tienen la misma cantidad de bolitas: 1.000.
En el vaso V quedaron 970 bolitas verdes que nunca fueron tocadas, más 27 azules que deposité la segunda vez que pasé la cuchara, más 3 verdes que volvieron. O sea, hay 973 verdes y 27 azules.

CONCLUSIONES:
a) en ambos vasos hay la misma cantidad de bolitas;
b) en el vaso V, hay 973 verdes y 27 azules;
c) en el vaso A, hay 973 azules y 27 verdes.
Como ve, hay la misma cantidad de verdes entre las azules que de azules entre las verdes. O, si se quiere, hay la misma cantidad de agua en el vino que de vino en el agua.

Final con moraleja incluida: para resolver este problema es obvio que no hace falta saber resolver ecuaciones, ni es necesario saber modelar con bolitas. Hay gente que llega a la respuesta razonando como en la primera solución. Y otra, razonando como en la segunda. O como en la tercera. Más aún: estoy seguro de que mucha otra gente lo resuelve de otras formas.
Por eso, no hay una única manera de resolver problemas. Lo que es interesante, es ser capaces de pensar. No importa tanto qué caminos uno toma, sino el resultado final. Todos iluminan.

Ojalá hayan llegado hasta acá. El libro es «Matemática, ¿estás ahi? Episodio 2. El autor(azo) es el Dr. Adrian Paenza y pueden descargarlo gratuitamente aquí.

Hasta el próximo vino.